Oscillations of a Stretched String

In a sonometer wire the tension is maintained by suspending a 50.7 kg mass from the free end of the wire. The suspended mass has volume of 0.0075m^​3. The fundamental frequency of the wire is 260Hz. Find the new fundamental frequency if the suspended mass is completely submerged in water

The fundamental frequencies of two copper wire of same length are in the ratio $1:2$. If the tension on the wires are$729 \mathrm{g}$ and $324 \mathrm{g}$ respectively, then the ratio of their diameters will be:

For an addition of $75 \mathrm{kg} \mathrm{wt}$ to the vibrating string raises the pitch by an octave of the original pitch then tension in string is

Look at the arrangement

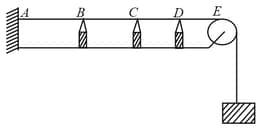
The fundamental frequency corresponding to the part of the string $AB$ is $600\mathrm{Hz}$, the fundamental frequency corresponding to the part $BC$ is $800\mathrm{Hz}$, the fundamental frequency corresponding to the part $CD$ is $1200\mathrm{Hz}$ and the fundamental frequency corresponding to the part $DE$ of the string is $2400\mathrm{Hz}$. If all the wedges are removed and the total string starts vibrating the frequency heard is $1200\mathrm{Hz}$. The string is vibrating in which overtone?

The tones that are separated by three octaves have a frequency ratio of

A person can hear frequencies only up to $10\mathrm{kHz}$. A steel piano wire $50 \mathrm{cm}$ long of mass $5 \mathrm{g}$ stretched with a tension of $400 \mathrm{N}$. The number of the highest overtone of the sound produced by this piano wire that the person can hear is

State the law of length of a vibrating string of a sonometre.

Plot a graph between frequency versus per unit length of a given wire under constant tension using a sonometre.

The graph between the frequency and the length of a given wire under constant tension using a sonometre is a

The fundamental frequency of a string is proportional to.

A frequency of a sonometer wire is $100 \mathrm{Hz}$. When, after making length of its wire twice, the tension is increased, then its frequency becomes $75 Hz$. The ratio of its initial and final tension is:

Two strings of a guitar are of lengths $40 \mathrm{cm}$ and $20 \mathrm{cm}$, such that they are made from same material and are of same thickness and under same tension. The frequency of longer wire is $250 \mathrm{Hz}$, and frequency of smaller wire is $f \mathrm{Hz}$. The value of $f$ is _____.

The frequency of third harmonic is given as $n=3n_0$, where $n_0$ is the fundamental frequency.

When string is plucked at one-sixth length from one end, the vibration produced in string is called third harmonic.

Select the incorrect option.

A segment of wire vibrates with fundamental frequency $400 \mathrm{Hz}$ under a tension of $8 \mathrm{kg}$ weight. The tension at which the fundamental frequency of the same wire becomes $800 \mathrm{Hz}$ is

The equation of a vibrating string, fixed at both ends, is given by $y=\left(3 \mathrm{mm}\right)\sin \left(\frac{\pi \mathrm{x}}{15}\right)\sin \left(400\pi \mathrm{t}\right)$ where $x$ is the distance (in cm) measured from one end of the string, t is the time (in seconds), and y gives the displacement. The string vibrates in $4$ loops. The speed of transverse waves along the string equals, for the fundamental mode,

Four wires of identical length, diameters and of the same material are stretched on a sonometre wire. If the ratio of their tensions is $1:4:9:16$ then the ratio of their fundamental frequencies are :-

What is the ratio of frequencies of the fundamental note produced in each of the two segments of an elastic wire that are cut into two pieces with a length ratio of $3:2$ and stretched with equal tension?

For definite length of wire, if the weight used for applying tension is immersed in water, then frequency will